Cách vẽ đồ thị parabol là kiến thức quan trọng trong toán học và ứng dụng trong đời sống. Vẽ biểu đồ parabol tuy khó nhưng lại rất dễ khi bạn chỉ cần hiểu một vài quy tắc và làm theo từng bước để vẽ đúng ngay lần đầu tiên. Xem hướng dẫn cách vẽ biểu đồ parabol chính xác dưới đây.
Vẽ parabol bằng thước kẻ và compa
Vẽ parabol bằng thước và compa được sử dụng rộng rãi vì tiện lợi và không khó thực hiện:
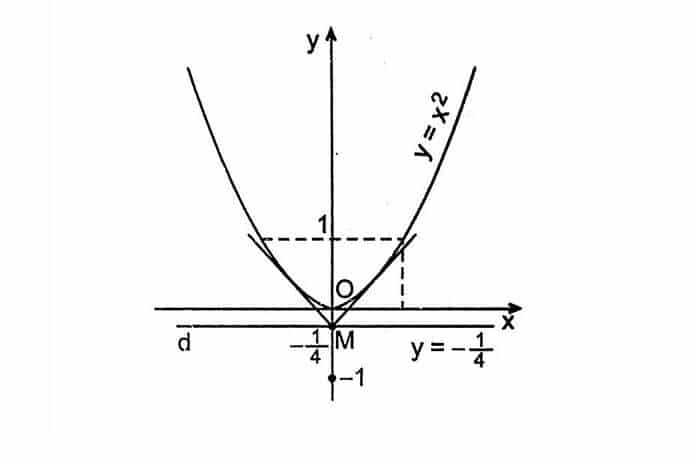
- Bước 1: Xét các điểm của parabol. Một mẹo hay là để những điểm này đối xứng với nhau để bạn có thể kiểm tra một bên của parabol.
- Bước 2: Vẽ trục Ox vuông góc với Oy tại điểm O.
- Bước 3: Trên trục Ox xác định điểm E và M sao cho M là trung điểm của OE. Ta có: OM=ME
- Bước 4: Tìm điểm M’ bất kỳ nằm trong ME, dùng thước thẳng vẽ đường thẳng đi qua M1 và song song với đường thẳng đã cho.
- Bước 5: Dùng la bàn quay một cung có bán kính bằng kích thước OM’. Điểm thuộc parabol là điểm giao nhau của cung và nằm trên đường thẳng song song với OM.
- Bước 6: Lấy thêm các điểm bất kỳ thuộc ME, sau đó thực hiện tương tự như các bước trên, dùng thước nối các điểm lại với nhau để tạo thành một parabol hoàn chỉnh.
Vẽ parabol bằng hàm bậc hai
Nhắc lại hàm bậc hai
Hàm số bậc hai có dạng:
y = ax2 + bx + c (a # 0)
Trong đó: a, b và c là các hằng số và a≠0
Đồ thị của hàm số bậc hai là một đường cong hình chữ U gọi là parabol/
Trong đồ thị hàm số bậc hai, hướng của parabol lên hoặc xuống phụ thuộc vào hằng số a. Nếu a<0 thì biểu đồ cau mày (mở) và nếu a>0 thì biểu đồ tạo ra một nụ cười (mở). Điều này được minh họa dưới đây:
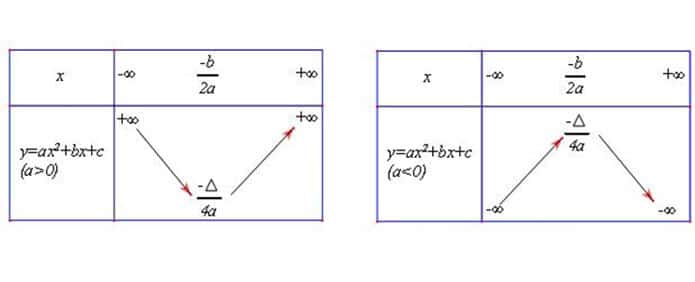
Đỉnh parabol
Một đặc điểm quan trọng của parabol là nó có một điểm cực trị, gọi là đỉnh. Nếu parabol hướng lên trên thì đỉnh biểu thị điểm thấp nhất trên đồ thị hoặc giá trị nhỏ nhất của hàm bậc hai. Nếu parabol mở xuống, đỉnh đại diện cho điểm cao nhất trên biểu đồ hoặc giá trị tối đa. Trong cả hai trường hợp, đỉnh tạo thành một bước ngoặt trên đồ thị.
Trục parabol đối xứng
Mỗi parabol có một trục đối xứng, song song với trục y. Trục đối xứng là đường thẳng đi qua đỉnh.
Giao điểm y
Giao điểm y là điểm mà parabol đi qua trục y. Không thể có nhiều hơn một trong các điểm này trên đồ thị của hàm bậc hai. Nếu đúng như vậy thì đường cong sẽ không phải là một hàm vì sẽ có hai giá trị Y cho một giá trị x, bằng 0.
Cách vẽ parabol bậc hai
- Bước 1: Xác định tọa độ đỉnh x=-b2a, y=-4a. Bạn có thể tìm tọa độ y bằng cách thay thế tọa độ x bạn tìm thấy vào hàm.
- Bước 2: Vẽ trục đối xứng đi qua đỉnh và song song với trục tung
- Bước 3: Tìm các điểm trên đồ thị bằng cách chọn giá trị x bất kỳ khác nhau, thay chúng vào phương trình ta sẽ tìm được các điểm y cho đồ thị hàm số.
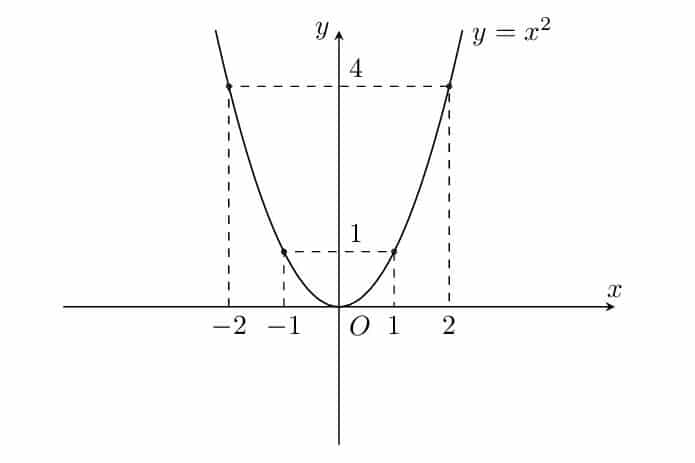
Bạn có thể tìm thấy nhiều điểm khác nhau cho đồ thị hàm số, độ chính xác của đồ thị phụ thuộc vào số lượng các điểm này. Bằng cách kết nối các điểm lại với nhau, chúng ta thu được hàm parabol bậc hai.
Cách viết phương trình parabol
Phương trình parabol có dạng:
y = ax2 + bx + c (a # 0)
Việc của bạn là tìm các hệ số a, b, c để thay thế trong công thức trên dựa vào bài toán cho sẵn hoặc đồ thị parabol có sẵn.
Dữ liệu mà vấn đề có thể cung cấp là:
- Xác định tọa độ I(x’,y’)
- Cho đồ thị parabol đi qua đỉnh A(x’, y’).
- Chứng minh rằng trục đối xứng là X=x’.
Có bao nhiêu loại thước parabol?
Thước Parabolic được thiết kế để kết hợp nhiều phương pháp tư duy nhỏ giúp vẽ đồ thị hàm số nhanh hơn và ít mắc lỗi hơn. Các loại thước parabol có hại là thước parabol nhỏ và lớn.
Thước parabol nhỏ

Thước parabol nhỏ thường được học sinh toán sử dụng. Giúp bạn dễ dàng quan sát và phân tích mối quan hệ giữa các tham số, từ đó đưa ra những suy luận phù hợp cho một đồ thị chính xác.
Thước parabol lớn
Đối với các đồ thị parabol hoặc hyperbol chứa các hàm đa thức bậc 2, 3 hoặc 5 thì cần có một thước đo chuyên dụng hơn và lớn hơn.

Thước parabol lớn thường được làm bằng nhựa dẻo, có màu trong suốt và có các ký hiệu chi tiết để hỗ trợ người đọc. Trên thước có 7 đường cong mẫu để vẽ đồ thị, trong đó có 5 đường vẽ đồ thị parabol có hệ số 2 và biến x (0,5; 1,0; 2,0; 4,0; 8,0) và 2 đường vẽ hyperbol. Với những đường cong nhất định, việc vẽ hình parabol trở nên dễ dàng và nhanh chóng hơn mặc dù kích thước của parabol rất lớn.




